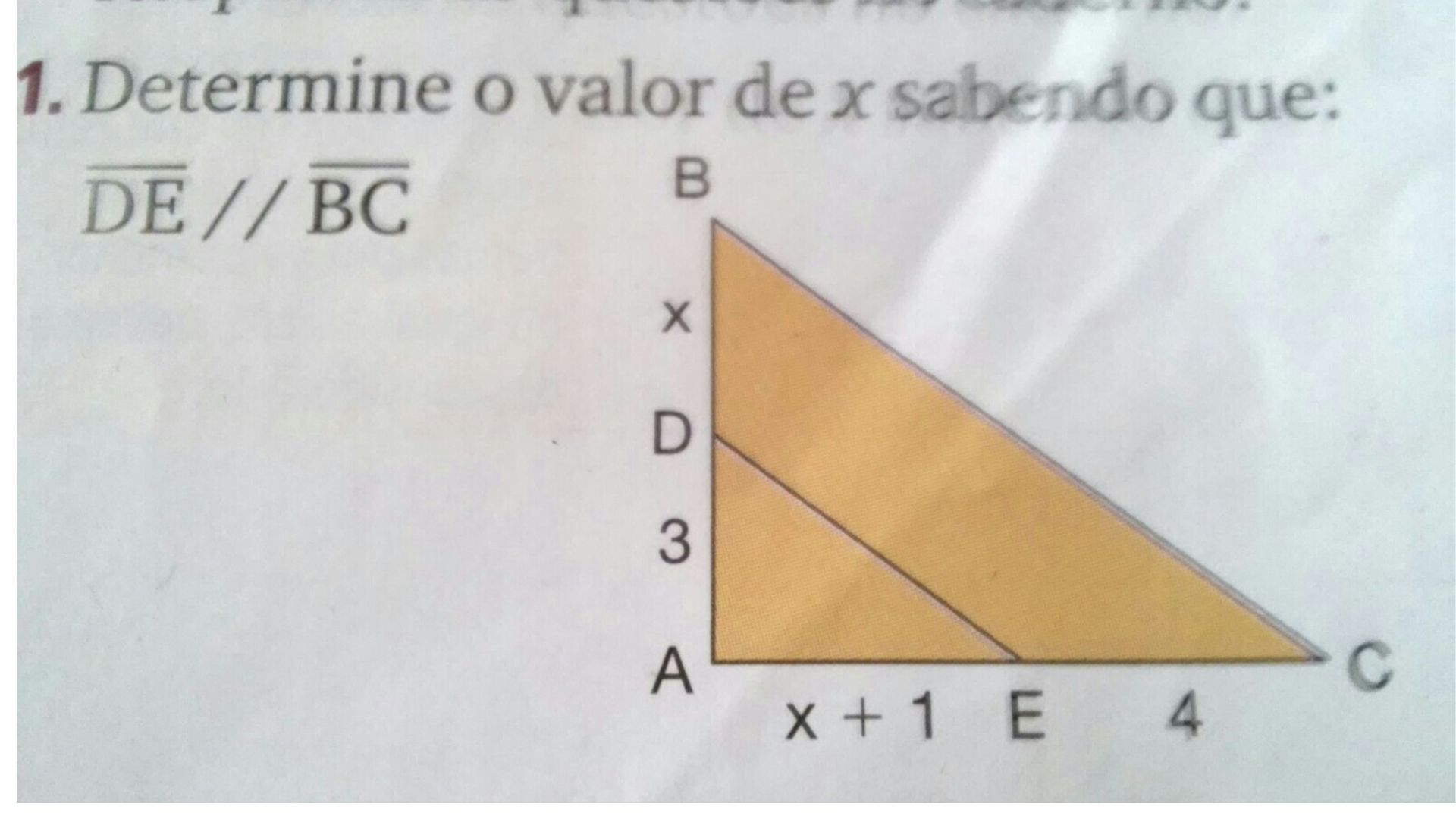
Introduction
In the world of geometry and mathematics, understanding the relationships between lines and angles is crucial. One fundamental concept that frequently arises is the determination of the value of ‘x’ when two lines are parallel. When two lines are parallel, they share some interesting properties that can help us find the value of ‘x’ and solve various geometric problems. In this article, we will explore parallel lines, transversals, and how to determine the value of ‘x’ when lines are parallel.
Parallel Lines and Transversals
Parallel lines are two straight lines in a plane that never intersect, no matter how far they are extended. In mathematical notation, we often use a double vertical bar (||) to represent parallel lines. When we have a pair of parallel lines, they create a set of angles that can be classified into different types:
- Corresponding Angles: These are angles that occupy the same relative position at each intersection of a transversal line. Corresponding angles are congruent, which means they have the same measure.
- Alternate Interior Angles: These are angles located on opposite sides of the transversal line and inside the two parallel lines. Alternate interior angles are also congruent.
- Alternate Exterior Angles: These are angles located on opposite sides of the transversal line and outside the two parallel lines. Like alternate interior angles, alternate exterior angles are congruent.
- Consecutive Interior Angles: These are pairs of angles that share a vertex and are located on the same side of the transversal line. Consecutive interior angles are supplementary, meaning their measures add up to 180 degrees.
Using these angle relationships, we can determine the value of ‘x’ in various scenarios involving parallel lines and a transversal.
Solving for ‘x’
To determine the value of ‘x’ when lines are parallel, follow these steps:
Step 1: Identify the type of angle relationship involved. Determine if the angle is corresponding, alternate interior, alternate exterior, or consecutive interior.
Step 2: Write an equation based on the angle relationship. For example, if you are dealing with corresponding angles, you can set up an equation like this: Angle 1 = Angle 2.
Step 3: Use the given information to solve for ‘x’. If you know the measure of one angle, you can substitute it into the equation to find ‘x’.
Let’s illustrate this with an example:
Example: Given two parallel lines and a transversal line as shown below:
cssCopy code
A B |----------| | | | x | | | |----------| C D
In this case, angle ‘x’ is an alternate interior angle to angle ‘A’. So, we can set up the equation: ‘x’ = Angle ‘A’.
If we know the measure of Angle ‘A’ (let’s say it’s 60 degrees), we can immediately determine that ‘x’ is also 60 degrees.
Conclusion
Understanding the properties of parallel lines and transversals is a fundamental skill in geometry and mathematics. It allows us to determine the value of ‘x’ and solve a wide range of geometric problems involving angles. By recognizing angle relationships such as corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles, we can set up equations and find the value of ‘x’ in various scenarios. So, the next time you encounter parallel lines and a transversal, remember these angle relationships to help you find the value of ‘x’ with ease.